Breitenkreisspezifische Temperaturen bei Strahlungsgleichgewicht

Angeregt von den Kommentaren und zu U.Webers Berichten über die Tagestemperaturen, die von einer direkten Sonneneinstrahlung erzeugt werden, versuchen manche Leser dies anhand von imaginierten Versuchen, anhand der Wirksamkeit des S-B Gesetzes, zu ergründen. Dies ist der einzige Möglichkeit der Wahrheit näher zu kommen. Hier ein Versuch, der einiges davon – allein mittels Strahlungstemperaturen – untersucht.

von Michael Mechtel

Zielsetzung und Motivation

Die Lebensbedingungen auf unserem Planeten Erde lassen sich letztlich auf die Einstrahlung von Energie durch die Sonne zurückführen. Diese Energie unterliegt vielfachen Umwandlungs- und Transportprozessen, an denen neben physikalischen auch chemische und biologische Vorgänge beteiligt sind. Nicht zuletzt die klimatischen Bedingungen, die wir vorfinden, gehen auf solche Prozesse zurück, und ein wichtiger, heutzutage häufig bemühter Parameter zur Charakterisierung des Klimas ist die Temperatur, sei es als regionale Temperatur mit ihren charakteristischen Schwankungen, sei es als zeitlicher und/oder räumlicher Mittelwert.

Zielsetzung dieses Artikels ist es, ein örtliches Temperaturniveau für die Regionen der Erde herauszuarbeiten, wenn allein der primäre Strahlungseinfluss der Sonne berücksichtigt wird und alle sekundären Nachfolgeeffekte (Transport und Umwandlung von Energie) beiseite gelassen werden. Die Anregung hierzu erfolgte durch die Artikel des Autors Uli Weber, der hier sein ‘hemisphärisches Stefan-Boltzmann-Modell‘ mehrfach vorgestellt hat. Die Schlussfolgerungen seines Modells werden aber nicht geteilt!

Beschreibung des Modells

Die genannte Zielsetzung und die Begrenzung des Rechenaufwandes erfordert ein sehr vereinfachtes Modell der Erde, das selbstverständlich nicht mehr die Realität abbildet, aber sehr wohl eine Basis für das Verständnis unserer Realität abgeben kann.

Zunächst erfordert es die Begrenzung des Rechenaufwandes, dass wir einen ideal kugelförmigen, homogenen Erdkörper voraussetzen, der auf einer exakten Kreisbahn in genau 365 Tagen die Sonne umkreist.

Um die genannten Sekundärprozesse von Energieumwandlung und –transport auszuschließen, sind auch einige physikalische Voraussetzungen erforderlich:

– Keine Atmosphäre vorhanden, damit also keine Luftströmungen

– Kein Wasser, damit also keine ozeanischen Strömungen und keine Phasenumwandlungen (Verdunsten, Kondensieren, Gefrieren, Schmelzen)

– Wärmeleitung vernachlässigbar klein

– Andere Energiequellen wie Restwärme aus dem Erdinneren oder die kosmische 3-K-Hintergrundstrahlung werden ebenfalls vernachlässigt.

Schließlich fordern wir noch eine schnelle Rotation dieser Modellerde, so dass sich keine nennenswerten Tag-Nacht-Unterschiede der Temperatur herausbilden können. Das bedeutet, dass jeder Punkt der Erdoberfläche zu jedem Zeitpunkt einzeln für sich im Strahlungsgleichgewicht mit der pro Erdumdrehung zugestrahlten Sonnen-Energie steht.

Weil die Erde um die Sonne umläuft, werden sich die Strahlungsbedingungen von Tag zu Tag ändern („Tag“ meint hier den bekannten Erdentag, also ein 365-stel Jahr). Da aber Wärmeleitung keine Rolle spielen soll, müssen wir keine Speichereffekte berücksichtigen, denn es wird nur eine dünne Oberflächenschicht an diesem Strahlungshaushalt beteiligt sein. Diese dünne Schicht kann sich schnell genug der sich ändernden Strahlungssituation anpassen, so dass das Strahlungsgleichgewicht von Tag zu Tag erhalten bleibt.

Auf dieser Voraussetzung beruhend, lässt sich die lokale Temperatur eines Oberflächenpunktes aus der momentanen Einstrahlung unter Anwendung des Stefan-Boltzmann-Gesetzes bestimmen. Es zeigt sich, dass diese Temperatur allein vom Breitenkreis und der Position der Erde auf ihrer Umlaufbahn abhängt. Jeder Breitenkreis weist damit einen eigenen Jahresgang der Temperatur auf.

Weitere Annahmen unseres Modells, angelehnt an unsere Realität:

– Albedo a = 0.3, selbstverständlich homogen auf der ganzen Oberfläche,

– Emissivität im Infraroten  = 0.95 (die Erde also nicht als schwarzer, sondern als dunkelgrauer Körper)

– Die Schrägstellung der Erdachse wird berücksichtigt.

Die breitenkreisspezifischen Temperaturverläufe wurden für diese Modellerde berechnet und sollen im folgenden dargestellt werden. Der Rechengang selber ist für Interessierte im Anhang skizziert.

Ergebnisse

Mit der extraterrestrischen Solarkonstante I₀ = 1361 W/m² und der genannten Albedo ergibt sich die maximal absorbierbare Intensität an der Oberfläche zu I_max = 953 W/m², was einer maximal möglichen Gleichgewichtstemperatur von 365 K = 92 ^oC entspricht (gerundete Werte).

1. Jahresgänge der Temperatur bei 23,45 Grad Achsneigung

Die Schrägstellung der Erdachse gegenüber der Erdbahnebene beträgt 23.45 Grad. Der damit sich ergebende Jahresgang der Temperatur unserer Modellerde auf verschiedenen Breitenkreisen der Nordhalbkugel ist in Abb. 1 dargestellt (für die Südhalbkugel gelten entsprechende Kurven, nur unter Vertauschung von Sommer- und Winterhalbjahr).

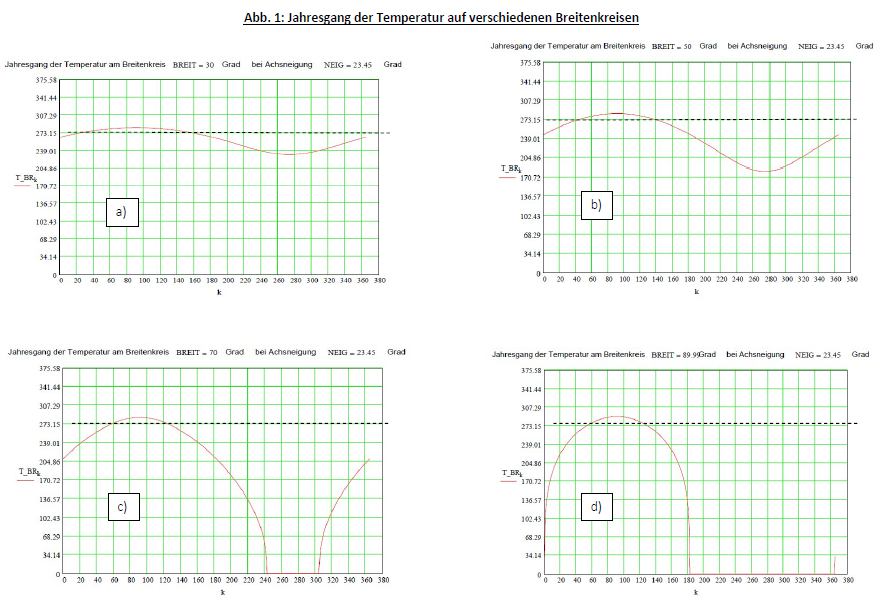
Auf der x-Achse ist die Tagesnummer aufgetragen, d.i. die Nummer des konventionellen Erdentages, beginnend mit Frühlingsanfang (21. März). Die Skala reicht bis 380, ein Jahr ist mit Nr. 365 beendet.

Auf der y-Achse ist die Absolut-Temperatur in der Kelvin-Skala aufgetragen, beginnend bei 0 K. Die gestrichelte Linie in den Diagrammen markiert den Nullpunkt der Celsius-Skala (273,15 K).

Bild a) gilt für den Breitenkreis 30 Grad.

Bild b) gilt für den Breitenkreis 50 Grad, das entspricht der Lage der Stadt Mainz. Man erkennt, dass der Unterschied zwischen Sommer- und Winterhalbjahr deutlich ausgeprägter ist als am 30. Breitengrad.

Bild c) gilt für den Breitenkreis 70 Grad. Diese Breite liegt nördlich des Polarkreises, deshalb tritt hier im Sommer Mitternachtssonne und im Winter Polarnacht auf. In der Polarnacht haben wir keine Sonneneinstrahlung, so dass die Temperatur rasch auf den absoluten Nullpunkt sinkt (würden wir die kosmische Hintergrundstrahlung in Betracht ziehen, lägen wir bei 3 K.)

Bild d) gilt für den „Breitenkreis“ 90 Grad, also den Nordpol. Hier haben wir ein halbes Jahr Mitternachtssonne (wechselnder Höhe) und ein halbes Jahr Polarnacht.

Insgesamt ist festzustellen, dass durchwegs, selbst in äquatornahen Gebieten, die Null-Grad-Celsius-Grenze kaum je überschritten wird, allenfalls um wenige Grad in den Sommermonaten. Zum Zweiten fällt in Regionen, die nicht von der Sonne beschienen sind, die Temperatur schnell sehr tief ab. Das macht sich in der zunehmenden Ausbeulung der Kurven nach unten im Winterhalbjahr bemerkbar, je weiter man sich vom Äquator weg in polnahe Regionen bewegt. Extrem wird es dort, wo Polarnächte auftreten.

2. Abhängigkeit des Temperaturganges von der Neigung der Erdachse

Man kann sich die Frage stellen, wie die Neigung der Erdachse sich auf den Verlauf der Temperaturwerte auswirkt. Dies wurde für den bereits in Abb. 1 aufgeführten 50. Breitengrad Nord untersucht, der exemplarisch für Deutschland stehen kann. Ergebnisse siehe Abb. 2.

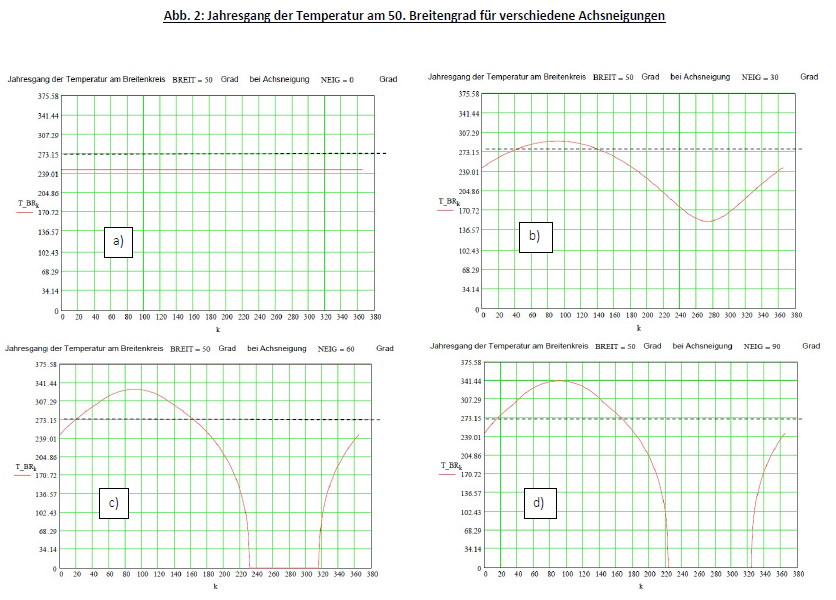
Die x- und y-Achsen sind die gleichen wie in Abb. 1.

Fall a) gilt für den Neigungswinkel 0 Grad. Hier steht die Erdachse senkrecht auf der Erdumlaufbahn. Damit ändert sich im Jahresverlauf nichts, es gibt keine Jahreszeiten (Annahme: die Sonne strahlt gleichmäßig in alle Richtungen).

Fall b) gilt für den Neigungswinkel 30 Grad. Der ist etwas größer, als es der Realität entspricht, die Jahreszeiten sind also etwas stärker ausgeprägt. Die Graphik ist mit der in Abb. 1 b) zu vergleichen, wobei sich zeigt, dass die Maximaltemperatur im Sommer leicht erhöht, die Winterdelle jetzt aber deutlich tiefer ausgeprägt ist.

Fall c) gilt für den Neigungswinkel 60 Grad. Der Polarkreis liegt dann bei 30 Grad, und das bedeutet, dass wir in Deutschland bereits Mitternachtssonne und Polarnacht erleben.

Fall d) gilt für den Neigungswinkel 90 Grad. Zur Sommersonnenwende zeigt die Erdachse also genau in Richtung Sonne, die Sonne steht über dem Nordpol, die höchsten Temperaturen treten auf. Beachte: auf der weiteren Umlaufbahn der Erde bleibt die Erdachse raumfest liegen! Das bedeutet: bei Herbstanfang liegt sie (ebenso wie bei Frühlingsanfang) tangential zur Erdbahn, und die Sonne steht nicht über dem Pol, sondern wandert über den Äquator. Beide Pole liegen auf der Grenze der beschienenen Erdhälfte. Im weiteren Verlauf wandert der Nordpol in die Polarnacht und der Südpol in die Mitternachtssonne. Auch die polnahen Gebiete der Nordhalbkugel erfahren eine Polarnacht.

Insgesamt fällt auf, dass die Stellung der Erdachse Einfluss auf die Höchsttemperatur im Sommer hat. Diese steigt, je größer der Neigungswinkel ist, weil dann die Sonne immer steiler über dem Horizont steht.

Dies kann jedoch nicht darüber hinwegtäuschen, dass die Minimaltemperatur im Winter immer tiefer fällt und damit die Jahresmitteltemperatur nach unten zieht, je schräger die Erdachse liegt.

Das Temperaturniveau liegt in allen Fällen sehr tief und selbst bei Neigungswinkel 0 Grad unterhalb der Null-Grad-Celsius-Marke. Dies soll zum Anlass genommen werden, Mitteltemperaturen näher zu untersuchen.

3. Extremal- und Mitteltemperaturen

Wir werfen einen Blick auf die mit dem Jahresgang verbundenen Maximal-, Minimal- und Mitteltemperaturen und beginnen wieder mit der Achsneigung 23.45 Grad aus Abb. 1. Ergebnisse siehe Tabelle 1 (gerundete Werte).

 

Extremale und mittlere Breitengrad-Temperaturen [K]
bei Neigung der Erdachse um 23,45 Grad
Breitengrad:	30	50	70	90
Maximum	283	284	286	290
Minimum	231	181	0	0
Jahresmittel	261	239	177	124

Tabelle 1

Die sommerlichen Maximalwerte nehmen mit dem Breitengrad etwas zu (von 10 auf 17 ^oC). Dies liegt daran, dass die Dauer der Nachtzeit abnimmt.

Die Jahresmittelwerte werden jedoch durch die winterlichen Minima umso mehr in die Tiefe gezogen, je weiter man nach Norden kommt. Sie liegen in der Tabelle zwischen -12 und -149 ^oC, auf dem 50. Breitengrad bereits bei ungemütlichen -36 ^oC. Es ist offensichtlich, dass wir hiermit weit entfernt sind von den realen Gegebenheiten, die wir kennen.

Angelehnt an Abb. 2 betrachten wir nun die Temperaturen in Abhängigkeit von der Neigung der Erdachse:

 

Extremale und mittlere Breitengrad-Temperaturen [K]
am 50. Breitengrad
Achsneigung:	0	30	60	90
Maximum	246	293	330	352
Minimum	246	151	0	0
Jahresmittel	246	235	198	194

Tabelle 2

Man erkennt einen Anstieg der sommerlichen Höchsttemperatur mit wachsender Achsneigung, was auf den immer steileren Sonnenstand und die zunehmende Sonnenscheindauer zurückzuführen ist. Der Bereich erstreckt sich von -27 bis +79 ^oC.

Aber auch hier zieht die zunehmende Nachtperiode die Jahres-Mitteltemperatur nach unten, der Bereich geht von -27 bis auf -79 ^oC.

Haben wir bisher breitenkreisspezifische Temperaturen und zusätzlich deren zeitliche Mittelung übers Jahr betrachtet, so wollen wir uns nun an eine räumliche Mittelung über die gesamte Oberfläche wagen. Diese lässt sich hier am Modell, im Gegensatz zur realen Erde, rechnerisch exakt durchführen. Exemplarisch zeigen wir den Jahresverlauf der globalen Mitteltemperatur am 50. Breitengrad für verschiedene Achsneigungen:

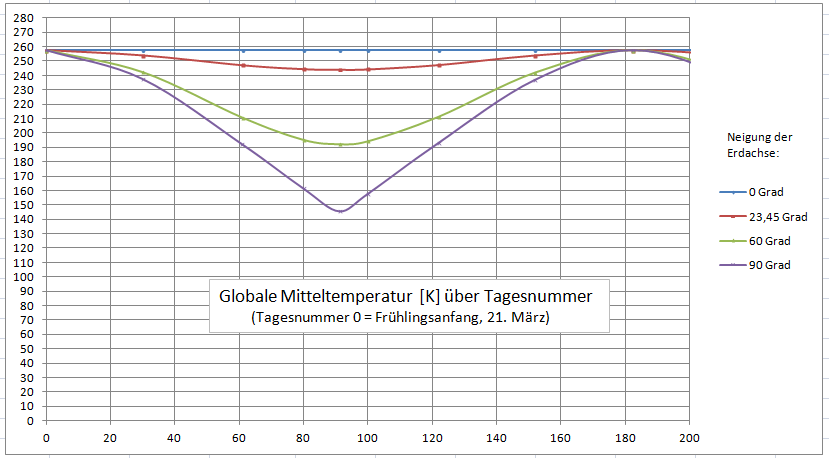
Abb.3: Halbjahresverlauf der globalen Mitteltemperatur am 50. Breitengrad

Bei Abb. 3 ist zu beachten, dass sie nur den Verlauf über ein halbes Jahr zeigt! Das nächste Halbjahr verläuft aus Symmetriegründen exakt genauso, wobei nur die Rolle von Nord- und Südhalbkugel vertauscht sind. Die x-Achse zeigt wieder die Tagesnummer, beginnend bei 0 (Frühlingsanfang) bis zur Tagesnummer 200, wobei das Halbjahr bei Nummer 182,5 (Herbstanfang) abgeschlossen ist.

Zunächst ist bemerkenswert, daß die Globaltemperatur überhaupt einen Jahresverlauf zeigt. Dieser ist besonders ausgeprägt bei 90 Grad Achsneigung und soll nun diskutiert werden. An den Äquinoktien (Frühlings- und Herbstanfang) ist die Globaltemperatur am höchsten und unabhängig von der Achsneigung. Die Sonne hat dann ihren Höchstand zur Mittagszeit senkrecht über dem Äquator, und kein Teil der Erde bleibt im Laufe einer Umdrehung unbesonnt, mit Ausnahme der beiden Pole, die aber nur punktförmig sind.

Das andere Extrem sind die Sommer- und die Wintersonnenwende: hier liegt ein Teil der Erde in der Polarnacht, am ausgeprägtesten bei 90 Grad Achsneigung, dann nämlich eine volle Erdhälfte. Da sich in der Polarnacht die Temperatur auf dem absoluten Nullpunkt einstellt, wird der globale Mittelwert stark nach unten gezogen, wie wir das auch schon in den Abschnitten 1 und 2 festgestellt haben.

Die Extremal- und Mittelwerte zu Abb. 3 sind in Tabelle 3 zusammengestellt. Wir erkennen wieder das Fehlen von Jahreszeiten bei Senkrechtstellung der Erdachse (0 Grad Neigung). Das globale Jahresmittel liegt hier – oh Wunder – bei den altbekannten (fast) 255 K. Dass es etwas mehr als 255 K sind, liegt daran, dass wir die Erde nicht als schwarzen, sondern als dunkelgrauen Körper behandeln (s.o.).

Sobald sich die Erdachse neigt, verschlimmert sich die Situation sogar noch: bei 23,45 Grad Neigung haben wir nur noch 250 K oder -23 ^oC Mitteltemperatur, und das senkt sich bei 90 Grad Achsneigung bis auf -70 ^oC ab.

Globale Mitteltemperatur [K]
in Abhängigkeit von der Achsneigung
Achsneigung:	0 Grad	23,45 Grad	60 Grad	90 Grad
Maximum	257	257	257	257
Minimum	257	244	192	145
Jahresmittel	257	250	221	203

Tabelle 3

Eine andere Erkenntnis lässt sich ebenfalls aus Tabelle 3 ziehen: in all den dort aufgeführten Fällen erhält die Erde als Ganze über eine Umdrehung hinweg zweifellos die gleiche Energie von der Sonne geliefert, nämlich genau den Energiebetrag, den sie während der Umdrehungszeit auf die Tagseite einstrahlt. Trotzdem unterscheiden sich die Globaltemperaturen! Berechnet man die Mitteltemperatur einfach aus der mittleren globalen Einstrahlung, wie es oft getan wird, kommt man in all diesen Fällen auf den gleichen Wert von 257 K.

Dass der aus der Globaleinstrahlung berechnete Wert i.d.R. nicht zutreffend ist – außer im Spezialfall senkrecht stehender Erdachse – liegt an der T-hoch-4-Abhängigkeit des Stefan-Boltzmann-Gesetzes. Dieser nichtlineare Zusammenhang hat zur Folge, dass es einen Unterschied macht, ob man wie hier Einzeltemperaturen berechnet und direkt über diese mittelt, oder ob man über die Einstrahlung mittelt und daraus eine Temperatur berechnet.

Der Fehler, den man mit letzterem Vorgehen macht, lässt sich anhand der Tabelle 3 quantifizieren: bei unserer Achsneigung von 23,45 Grad beträgt er +7 K oder, relativ ausgedrückt: 7/273 = 2,5 %.

Bei 90 Grad Achsneigung beträgt der Fehler (257 – 203) K = 54 K oder 54/273 = 19,9 %. Er ist deswegen größer, weil auch die Temperaturspanne, über die gemittelt wird, größer ist (vgl. Abb 1 b mit Abb. 3 c).

Zusammenfassung und Diskussion

Wir haben die Temperaturen untersucht, die sich auf der Erdoberfläche einstellen, wenn wir alle sekundären Einflußfaktoren ausschalten und uns allein auf die Sonne als primäre Energiequelle und das Strahlungsgleichgewicht der Erde mit ihr bzw. dem Weltall konzentrieren.

Zusammenfassend fällt dabei ins Auge, dass die Oberflächentemperaturen, die uns die Sonne unter diesen Umständen spendieren kann, weit unter dem Temperaturniveau liegen, welches wir real auf unserer Erde vorfinden! In Deutschland würden selbst im Hochsommer maximal nur rund 10 ^oC erreicht. Das liegt daran, dass wir in unserem Modell eine ungehinderte Abstrahlung ins Weltall haben und keinerlei Puffer- und Ausgleichseffekte für die Wärme.

Daraus wird ersichtlich, welch große Rolle all die Sekundäreffekte spielen, die wir im Modell ausgeschlossen haben: an vorderer Stelle zweifellos die riesige Wärmespeicherung in den Ozeanen und die Ausgleichsprozesse durch Wärmetransport in den Meeres- und Luftströmungen. Und nicht zuletzt müssen wir der Atmosphäre eine erhebliche Schutzfunktion gegenüber der Auskühlung zugestehen. Die kann nur in einer Behinderung der Abstrahlung bestehen, die landläufig unter dem Stichwort Treibhauseffekt bekannt ist.

Oft wird dagegen eingewandt, dass der Erdboden direkt von der Sonne erwärmt wird und die kühle Atmosphäre nicht den warmen Erdboden noch weiter erwärmen könnte. Doch, sie kann! Indem sie nämlich als Hindernis für die Abstrahlung fungiert. Das lässt sich vergleichen mit dem Anziehen einer Wollmütze im Winter. Kann die kühle Wollmütze die warme Kopfhaut erwärmen? Ja, sie kann es indirekt. Die eigentliche Heizquelle für die Kopfhaut ist natürlich der warme Blutkreislauf. Aber die Wollmütze stellt ein Hindernis für die Wärmeabgabe nach draußen dar, und das beschert der Kopfhaut eine höhere Temperatur und dem Träger ein wohliges Gefühl. Anderes Beispiel: Jeder Bauphysiker weiß, dass die Außendämmung einer Hauswand bei gegebener Heizleistung im Inneren die Wandtemperatur anhebt.

Auf die einzelnen Mechanismen des Treibhauseffektes und die beteiligten atmosphärischen Komponenten einzugehen, lag nicht in der Zielsetzung dieser Arbeit. Insbesondere die Rolle des CO2 wird nicht behandelt. Als gute Quelle hierfür lässt sich der Vortrag von Prof. Ganteför heranziehen, der kürzlich von EIKE präsentiert wurde: https://eike-klima-energie.eu/2024/02/24/treibhauseffekt-und-waermestau-auf-der-erde/

Bei der Untersuchung hat sich gezeigt, dass die Neigung der Erdachse ebenfalls die Oberflächen-Temperaturen beeinflusst, und zwar sowohl den Jahresverlauf als auch den Mittelwert.

Nachbemerkung

Schließlich noch eine allgemeine Bemerkung zur Temperaturmittelung: es wurde hoffentlich klar, dass dieses Verfahren seine Berechtigung hat. In Deutschland leben wir auf mittleren Breiten in einer gemäßigten Klimazone. Wir haben ein allgemeines Temperaturniveau von geschätzt etwa 10 ^oC, um das sich die tatsächlichen Temperaturen übers Jahr gruppieren. Man bemerke, dass insoweit noch nicht von Mittelung die Rede ist (auch wenn Meteorologen einen auf Messreihen beruhenden Mittelwert nennen, der nicht weit von diesen 10 ^oC entfernt ist). Vergleicht man nun dieses Temperaturniveau mit dem breitengradtypischen Mittelwert von 239 K oder -34 ^oC aus unserem Modell (Tabelle 1), so sollte auch dem hartgesottensten Mittelungsskeptiker einleuchten, dass diesem Parameter eine Aussagekraft zukommt. Im vorliegenden Fall die, dass das Modell nicht die Realität beschreibt.

Im Prinzip ist der Parameter auch zur Beurteilung von IPCC-Modellen brauchbar, wenn sich eine Möglichkeit findet, deren Ergebnisse mit der Empirie abzugleichen.

Anhang: Berechnungsmethode

Grundlage für die Berechnung der Temperatur im Strahlungsgleichgewicht ist die an der Oberfläche absorbierte Energie-Flussdichte , auch Intensität genannt und meist in W/m² angegeben. Deren Wert für senkrechte Einstrahlung haben wir mit _max = 953 W/m² angesetzt. Bei Schrägeinstrahlung unter dem Winkel h erhält man

 = _max * sin(h). h ist eine Koordinate im Horizontsystem und wird auch als Elevation der Sonne bezeichnet.

Zur Erklärung astronomischer Koordinaten sei auf die Fachliteratur verwiesen, s. z.B. die Quellenangaben.

Die Bestimmung von h im Jahres- und Tagesverlauf gelingt durch Rückgriff auf das ruhend-äquatoriale Koordinatensystem (, t). Dafür gibt es die grundlegende Gleichung [1], [2]

sin(h) = sin() * sin() + cos() * cos() * cos(t). ()

 ist der betrachtete Breitengrad, die ruhend-äquatorialen Koordinaten sind  und t, also Deklination und Stundenwinkel der Sonne. Alle Winkel sind im Bogenmaß zu verstehen.

sin wiederum hängt von der Position der Erde auf ihrer Umlaufbahn (hier: Kreisbahn) ab. Numeriert man die Tage ab Frühlingsanfang mit der Tagesnummer TNR, dann ist der zugehörige Ekliptikwinkel der Erde auf ihrer Kreisbahn, von der Sonne aus betrachtet,  = TNR/365 * 2. Damit und mit dem Neigungswinkel  der Erdachse gegen die Erdbahnebene (Schiefe der Ekliptik) erhält man sin() = sin() *sin() [3].

Um die mittlere Intensität  auf Breitengrad  am Tag TNR zu bestimmen, muss man (h) unter Einsetzen von Gleichung () über eine Erdumdrehung integrieren und das Ergebnis auf die zu  gehörige Ringfläche verteilen. Für die Integrationsgrenzen wird der Stundenwinkel t₀ der Sonne bei Sonnenaufgang benötigt.

Bei der Bestimmung von t₀ ist eine Fallunterscheidung erforderlich: man erhält t₀ durch Nullsetzen von Gleichung () für Breitengrade unterhalb der Polarregion, wo weder Mitternachtssonne noch Polarnacht herrschen. Der Grenzbreitengrad, der die Polarregion vom Rest abtrennt, hängt natürlich vom Datum ab und bestimmt sich zu _grenz = /2 – ||. Oberhalb _grenz ist t₀ =  zu setzen.

Die zu  gehörige Gleichgewichtstemperatur berechnet man schließlich nach Stefan-Boltzmann zu

T = ( / ( * ))^0.25. Für einen schwarzen Körper wäre die Emissivität  = 1, wir haben uns aber für den Wert 0,95 entschieden.  = 5,67E-8 W / (m² * K⁴) ist die Stefan-Boltzmann-Konstante.

Für die Jahresgänge der Abb. 1 und 2 wurden nach diesem Schema die täglichen Temperaturen über ein Jahr berechnet. Hierfür wurde die Mathematik-Software Mathcad 2000 Professional verwendet.

Die Globaltemperatur-Kurven der Abb. 3 wurden mit Hilfe von Microsoft EXCEL gewonnen, indem für eine Anzahl von Stütztagen die Gleichgewichts-Temperatur aller Breitenkreise mit Schrittweite 1 Breitengrad berechnet und daraus der Mittelwert gebildet wurde. Die dargestellten Kurven sind zwischen den Stütztagen interpoliert. Die globalen Mittelwerte aus Tabelle 3 wurden näherungsweise ebenfalls mittels Stütztagen abgeschätzt.

Quellen

[1] Keller, H.-U.: Astrowissen, Stuttgart 1994

[2] https://de.wikipedia.org/wiki/Astronomische_Koordinatensysteme

[3] E. Boeker, R. v. Grondelle: Physik und Umwelt, Braunschweig 1997