Kevin Kilty
Die am meisten kommentierten Beiträge auf WUWT betreffen alles, was mit Wärmestrahlung zu tun hat, und ihre fast unerträgliche Länge resultiert aus dem, was ich nur als Gezänk bezeichnen kann. Der Artikel hierzu von vor einigen Tagen enthielt jedoch einige wertvolle Hinweise, welche die Grundlage für diesen Aufsatz bilden. Ich hoffe, dass wir heute nicht noch einen längeren Thread aufmachen werden.
Eines das immer wieder auftaucht ist der Streitpunkt ist das Dogma, dass alle Objekte und Substanzen bei jeder endlichen Temperatur Infrarotstrahlung aussenden. Zu diesem hartnäckigen Dogma äußerte sich ein Kommentator wie folgt:
„Ich vermute, dass ihm, wie mir, in seiner Ausbildung beigebracht wurde, dass ALLE Dinge thermisches IR ausstrahlen. Ich vermute, das gilt für uns alle. Ich vermute auch, dass es interessant wäre, einige ältere Texte durchzusehen, um festzustellen, wann genau die Verwischung des Strahlungsverhaltens zwischen ‚Dingen‘ (Objekten) und atmosphärischen Gasen begann.“
In der Tat gilt das wahrscheinlich für uns alle. Zweifellos habe ich dies auch einmal geglaubt. Selbst nachdem ich meine Ansicht vor Jahrzehnten geändert habe, habe ich unvorsichtige Aussagen gemacht, die nicht immer zur Klärung der Dinge beigetragen haben. Aber zum Trost kann ich auf fehlerhafte Aussagen der NASA wie diese verweisen:
Wie Atmosphärensonden funktionieren
Alles, was eine Temperatur hat, strahlt. Wir strahlen. Eiszapfen, Schwimmbäder und Tannenbäume strahlen. Das gilt auch für die Moleküle aller Gase, aus denen die Atmosphäre besteht.“ [1]
Hier ist eine noch schwierigere Aussage, die halb richtig und halb völlig falsch ist. Sie steht in einem Lehrbuch, mit dem ich unterrichtet habe, Fundamentals of Heat and Mass Transfer, Incropera and Dewitt.
„Für nicht polare Gase wie O₂ oder N₂ ist eine solche Vernachlässigung gerechtfertigt, da die Gase keine Strahlung abgeben und für einfallende Wärmestrahlung im Wesentlichen transparent sind….“ (S. 896 in der 7. Auflage).
Es ist absolut richtig, dass Stickstoff keine IR-Strahlung aussendet. Warum ist sie nur halb so falsch? Finden wir es heraus…
In Anlehnung an die obige Diskussion wollen wir uns nun mit der Wechselwirkung von Strahlung und Materie befassen. Dies ist ein außerordentlich kompliziertes Thema. Mit ein paar einfachen Modellen und deren Anwendung auf eine Reihe von Materialien lässt sich jedoch eine ganze Menge verstehen.
Der elektrische Dipol
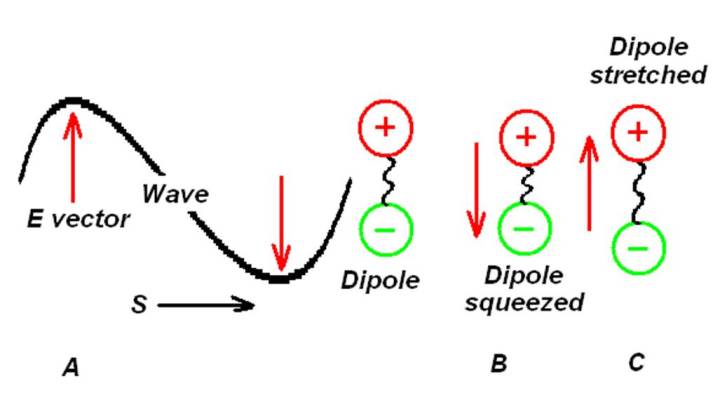
Abbildung 1 zeigt eine EM-Welle, wobei S ihren Poynting-Vektor oder Ausbreitungsvektor angibt. Aus der Sicht eines stationären Dipols, der aus einer positiv geladenen Masse besteht, die von einer anderen, durch eine Feder verbundenen negativ geladenen Masse getrennt ist, ist die EM-Welle ein elektrisches Wechselfeld. Der Dipol ist ein Modell einer gasförmigen molekularen Substanz, wobei die Massen für die Atome stehen und die Feder die molekulare Bindung darstellt. Wir können dieses Modell mit rein klassischer Dynamik behandeln, oder als semiklassisch, indem wir die Dynamik der Massen und der Feder quantisieren oder als vollständig quantenmechanisch ansehen, und kommen zu den gleichen Schlussfolgerungen.
Wenn die EM-Welle (A) vorbeizieht, sieht unser Atom zunächst einen nach unten gerichteten elektrischen Feldvektor, der die beiden Massen zusammenpresst (B), dann einen nach oben gerichteten elektrischen Feldvektor, der sie auseinanderzieht (C), und so weiter. Der Durchgang der EM-Welle versetzt den Dipol in Schwingung, was auch bedeutet, dass ihm Energie zugeführt wird.
Am effektivsten ist die Energiezufuhr, wenn die Frequenz der durchlaufenden Aufwärts-/Abwärtsbewegung mit der Resonanzfrequenz der Massen und der Feder übereinstimmt. Es versteht sich von selbst, dass ein bereits in Bewegung befindlicher Dipol seine Energie wieder an das EM-Feld abgeben könnte, wenn die Phasendifferenz zwischen einer vorbeiziehenden Welle und dem Dipol so groß wäre, dass die Welle die betreffende Energie aufnehmen könnte.
Die Quantenmechanik verändert dieses Bild nur geringfügig. Anstelle eines Oszillators, der eine beliebige Energiemenge absorbieren kann, hat ein Molekül zulässige Energieniveaus der Schwingung, und das quantisierte EM-Feld muss die richtige Energiemenge bereitstellen, um den Oszillator von einem zulässigen Energieniveau zu einem anderen zu bewegen. (Wir werden die Komplikation der Linienbreite ignorieren.)
Die wesentlichen Merkmale der Wechselwirkung sind jedoch zu erkennen. Das vorbeiziehende elektrische Feld (EM-Welle) hat einen elektrischen Feldvektor (E), und die Materie steuert einen Dipol bei, der in der Lage ist, an das EM-Feld anzukoppeln. Ein Molekül, das keinen Dipol besitzt, ist bei dieser sehr wichtigen Wechselwirkung benachteiligt.
Welche Moleküle in der Atmosphäre werden dadurch ausgeschlossen?
Argon mit Sicherheit, denn es ist ein einatomiges Edelgas. Es hat nur eine Masse und überhaupt keine Feder. Ganz gleich, wie man diese Situation betrachtet, die Edelgase haben keine Möglichkeit, an ein EM-Feld zu koppeln. Jedenfalls nicht im Infraroten. Man muss auf sehr energiereiche Strahlung warten, die in der Lage ist, an elektronische Bahnen im sichtbaren und ultravioletten Bereich zu koppeln. Wie Willis erläuterte, ist die Spülung eines IR-Spektrometers mit Argon zur Vermeidung von Störsignalen ein Experiment, das eindeutig zeigt, dass einige Materialien keine IR-Strahlung abgeben.
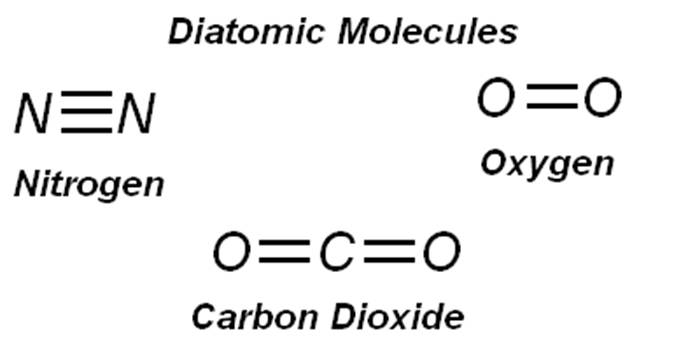
Sieht man einmal von den Isotopen ab, so hat Stickstoff zwei identische Moleküle, die kovalent miteinander verbunden sind; diese Bindung hat keinen ionischen Charakter, so dass Stickstoff von der Wechselwirkung mit einem EM-Feld bei IR-Wellenlängen ausgeschlossen ist. Auch Sauerstoff ist ein kovalent gebundenes Molekül und nimmt nicht an den Wechselwirkungen mit einem IR-EM-Feld teil.
Nun ist CO₂ interessant. Abbildung 2 zeigt das CO₂-Molekül. Es ist linear und symmetrisch. Jeder Sauerstoff ist kovalent an den Kohlenstoff gebunden. Es scheint also, dass dieses Molekül nicht an ein EM-Feld koppeln kann. Die kovalenten Bindungen sind jedoch nicht vollkommen, sondern aufgrund des Unterschieds in der Elektronegativität von Kohlenstoff (2,55) im Vergleich zu Sauerstoff (3,44) hat die Bindung einen kleinen ionischen Charakter. Bei einem Elektronegativitätsunterschied von nur 0,89 wird die Bindung als polar-kovalent bezeichnet. Daher kann das gesamte Molekül, das im obigen Incropera-Zitat nicht polar ist, dennoch eine Kopplung eingehen, und zwar im Fall von CO₂ mit einem EM-Feld, da die Details des Moleküls effektive Dipole enthalten.
Der magnetische Dipol
Molekularer Sauerstoff ist, obwohl er kovalent gebunden ist, ein wenig seltsam. Trotz seiner Ähnlichkeit mit Stickstoff hat jeder Sauerstoff im Molekül in seinem Grundzustand ein ungepaartes Elektron – ein Zustand, der als Triplett bekannt ist (zwei gepaarte und ein ungepaartes Elektron). Molekularer Sauerstoff ist ein Diradikal. Der Elektronenspin und der Bahndrehimpuls des ungepaarten Elektrons verleihen dem Sauerstoff im Grundzustand einen magnetischen Dipol – so etwas wie einen magnetisierten Kreisel. Dies wiederum ermöglicht es dem Sauerstoff, sich an einem lokalen Magnetfeld auszurichten. Dies ist der Grund dafür, dass Sauerstoff in besonderem Maße paramagnetisch ist.
Sauerstoffmoleküle sind, wie alle anderen Moleküle in der Atmosphäre, ständig Kollisionen ausgesetzt, wodurch die Gleichgewichtsausrichtung des magnetischen Dipols gestört wird. Sobald der magnetische Dipol gestört ist, versucht er, sein Gleichgewicht wiederherzustellen, und zwar durch Präzession um ein Orientierungsfeld mit einer festen Frequenz im Mikrowellenbereich (etwa 60 GHz). Mit anderen Worten: Das Signal, das der magnetische Dipol aussendet, hängt davon ab, dass der komplexe Zustand der Atmosphäre ein wenig aus dem Gleichgewicht geraten ist.
Eine höhere Temperatur führt zu einer höheren Kollisionsrate, einem größeren Ungleichgewicht und einer größeren Signalstärke, die manchmal auch als Helligkeit bezeichnet wird. Durch die Messung der Helligkeit bestimmter Mikrowellenfrequenzen können Satelliten die atmosphärische Temperatur bestimmen. Die Helligkeit dieser Signale wird jedoch in Mikrowatt pro Quadratmeter und Steradiant Raumwinkel gemessen – nützlich für Messungen, aber vernachlässigbar für den Energietransport.
Kondensierte Materie
Der größte Unterschied zwischen gasförmigem Material und kondensiertem Material besteht darin, dass in kondensiertem Material jedes Molekül stark von allen anderen Molekülen in unmittelbarer Nähe beeinflusst wird. Dies führt dazu, dass die Absorption und Emission von Strahlung in breiten Bändern oder Kontinua stattfindet und nicht in diskreten Frequenzen. Häufig wird angenommen, dass dies bedeutet, dass kondensierte Materie wie ein Schwarzer Körper nach dem Stefan-Boltzmann-Gesetz (SB) strahlt. Einige Hintergrundinformationen zum SB-Gesetz sind hier angebracht.
Zwei Strahlungsgesetze sind hier von Bedeutung. Der Energieerhaltungssatz besagt, dass das Transmissionsvermögen (t), das Absorptionsvermögen (a) und das Reflexionsvermögen (г) die Beziehung t+a+r = 1 erfüllen müssen. Die Kirchhoff’sche Regel besagt, dass Emissionsgrad und Absorptionsgrad bei jeder Frequenz gleich sind (a=ε). Somit ist ε+r+t=1 bei einer bestimmten Frequenz.
Was wir häufig als Schwarzkörperstrahlung bezeichnen, wurde ursprünglich als Hohlraumstrahlung bezeichnet. In einem Hohlraum mit sehr kleinem Ausgang ist t gleich Null, weil der Hohlraum undurchsichtig ist; r ist gleich Null, weil der Ausgang so winzig ist, dass die eintretende Strahlung erst nach sehr vielen Reflexionen entweicht, und somit ist a=ε=1. Aus Plancks Bemühungen, aber auch als Ergebnis aus der klassischen Thermodynamik, ist die emittierte Leistung in dieser Hohlraumstrahlung W=σT⁴, das SB-Gesetz.
Wenn wir nun auf den Hohlraum verzichten, indem wir die kondensierte Materie zu einer Oberfläche öffnen, gilt dann immer noch das SB-Gesetz? Offensichtlich hängt SB von so vielen Reflexionen in einem Hohlraum ab, dass im Grenzfall die gesamte Strahlung absorbiert wird (ε=1). Im Gegensatz dazu tritt an einer offenen Oberfläche nur eine Reflexion auf, was bedeutet, dass das tatsächliche Reflexionsvermögen des Materials jetzt wichtig ist.
So haben Metalle, die oft reflektierend sind, einen effektiven ε-Wert von weniger als 1. Gold zum Beispiel hat, wenn es gut poliert ist, einen Emissionsgrad von 0,02 bis 0,05. Gold kann jedoch sehr emittierend sein, wenn seine Oberfläche durch Bearbeitung porös gemacht wird, was als Schwarzgold bekannt ist. Es bietet nun eine Oberfläche, an der EM-Energie in „Schluchten“ fallen kann, um eine Analogie zu bilden, und effektiv absorbiert wird. Die Oberflächenbeschaffenheit eines beliebigen Materials kann also einen bestimmten Emissionsgrad bewirken.
Genau wie bei Molekülen, die keinen Dipol haben, der an ein EM-Feld koppelt, können auch kondensierte Materialien keinen Dipol haben. Diamant zum Beispiel hat eine hochsymmetrische Struktur mit ausschließlich kovalenten Bindungen. Sein IR-Emissionsgrad ist sehr niedrig; in einer Tabelle wird er mit 0,02 angegeben. Er ist nicht reflektierend, sondern hochtransparent mit nur zwei Fällen von Zwei-Photonen-Absorption bei 2,5 und 6,5 Mikrometern. Quarz hingegen, der oberflächlich betrachtet wie Diamant aussieht, besteht hauptsächlich aus kovalenten Silizium-Sauerstoff-Bindungen. Wie bei CO₂ sind die Bindungen jedoch aufgrund der unterschiedlichen Elektronegativität von Silizium (1,90) und Sauerstoff (3,44) praktisch polar. Quarz hat einen Infrarot-Emissionsgrad über 0,9.
Natürliche Erdmaterialien
Materialien wie Wasser, Eis und Schnee enthalten Dipole aus dem Wasser selbst. Sie sind stark absorbierend und emittierend. Felsen und nackter Boden bestehen in der Regel aus Silikatmineralien und haben eine raue Oberfläche aus losen Partikeln, an der Mehrfachreflexionen die Absorption und Emission begünstigen; der Emissionsgrad liegt im Allgemeinen über 0,90. Bepflanzte Böden sind gelegentlich feucht, und ihr Reflexionsvermögen wird durch Streuung innerhalb der Vegetation verringert. Sie sind hoch emittierend.
Das Ergebnis ist, dass ein großer Teil der Erdoberfläche aufgrund der Zusammensetzung, der Rauheit, des Wassers oder der Vegetation bei IR-Wellenlängen fast ein schwarzer Körper ist. MODTRAN zum Beispiel verwendet für alle seine Standardberechnungen einen Oberflächen-Emissionsgrad von 0,971.
Die Modellatmosphäre
Eine Reihe von Personen, die sich zu diesen Themen äußern, sprechen von der Thermalisierung der Schwarzkörperstrahlung. In der üblichen Verwendung dieses Wortes würde das bedeuten, dass die Strahlung in irgendeiner Weise mit ihrer Umgebung ins Gleichgewicht kommt. Ich vermute, dass damit gemeint ist, dass die Strahlung des Schwarzen Körpers in eine der örtlichen Temperatur entsprechende Bewegungsverteilung der materiellen Bestandteile der Atmosphäre umgewandelt wird, d. h. die Strahlung verschwindet schnell in kinetische Energie.
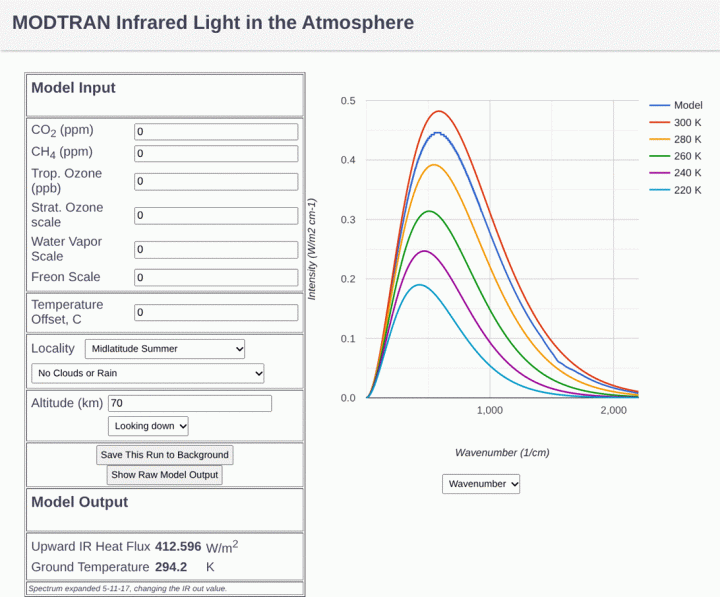
Betrachten wir eine Atmosphäre, die nur aus Stickstoff besteht. Man kann sie in einem Hohlraum unterbringen, der als Wärmebad dient, um sie auf einer Temperatur von, sagen wir, 300 K zu halten. Obwohl der Hohlraum mit Schwarzkörperstrahlung gefüllt ist, kommt es zu keiner Wechselwirkung der Strahlung mit dem Stickstoff, da der Stickstoff keinen Dipol besitzt und keine Möglichkeit hat, an das EM-Feld zu koppeln. Abbildung 3 zeigt, was ein IR-Spektrometer auf Satellitenebene beim Blick auf die Erdoberfläche in diesem Fall erkennen würde – eine reine Schwarzkörperkurve bei einer Temperatur von 294,2 K:
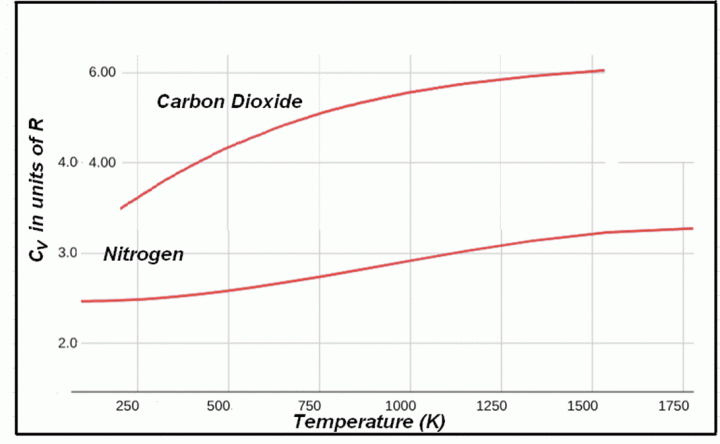
Abbildung 4 zeigt die Wärmekapazität bei konstantem Volumen für Stickstoff und Kohlendioxid zwischen 200 K und 1800 K. Von 200 K bis etwa 400 K ist die Kurve für Stickstoff sehr flach und gleich 5/2 R, wobei R die Gaskonstante ist. Nach der kinetischen Gastheorie bedeutet dies, dass eine Stickstoffatmosphäre bei typischen Erdatmosphären-Temperaturen von 200-300 K fünf Freiheitsgrade hat – drei Translationen in x, y und z sowie zwei Rotationen sind voll an der Energiespeicherung beteiligt, und die durchschnittliche Energie pro Stickstoffmolekül beträgt 5 kT, wobei k die Boltzmann-Konstante ist. Bei 300 K sind dies 2×10-20 J oder etwa 0,13 eV pro Atom. Schwingungszustände treten bei Stickstoff erst bei viel höheren Temperaturen auf.
Kohlendioxid hingegen weist bei 300 K einen Cv-Wert auf, der auf die Beteiligung von etwa sechs Freiheitsgraden oder etwas mehr hinweist, also auf die Aktivität von drei Translationsmoden, zwei Rotationen und einer oder mehreren Vibrationen. Die Steigung der Kurve deutet darauf hin, dass mehr Schwingungsfreiheitsgrade schnell wirksam werden.
Hinzufügen von CO₂ zu unserer Modell-Stickstoffatmosphäre
CO₂ hat drei Schwingungsmoden im IR-Teil des Spektrums. Der symmetrische Streckmodus (n1), der entartete Biegemodus von CO₂ (n2) und der asymmetrische Streckmodus (n3) können alle durch Kollisionen mit N₂-Gas angeregt werden. Die durchschnittliche kinetische Energie pro Freiheitsgrad beträgt bei 300 K etwa 2×10-21 J oder 0,013 eV, und die am wenigsten energiereiche Schwingungsform von CO₂ (n2) benötigt 1,3×10-20 J oder 0,08 eV. Eine andere Betrachtungsweise ist, dass die Äquivalenttemperatur im n2-Zustand etwa 960 K beträgt, so dass selbst bei einer Gastemperatur von 300 K die energiereicheren N₂-Moleküle in der (Maxwell-)Geschwindigkeitsverteilung in der Lage sind, ein CO₂-Molekül im Grundzustand während einer Kollision in einen angeregten n2-Zustand zu versetzen. Betrachtet man CO₂ als Zwei-Niveau-Atom, so zeigt der Boltzmann-Faktor e↑∆E/kT an, dass sich etwa 4 % der Stickstoffmoleküle im Gleichgewicht bei 300 K im n2-Zustand befinden würden. Die Tatsache, dass der n2-Zustand bei einem Zusammenstoß rascher als bei einer Emission entregt wird, spielt keine Rolle, da die detaillierte Bilanz verlangt, dass der umgekehrte Fall genauso häufig eintritt.
Durch die Zugabe von CO₂ haben wir nun eine Atmosphäre, die in andere Teile des Gases, auf die umgebende Oberfläche oder durch ein Fenster strahlen kann. Ein sich außerhalb des Gaskörpers befindendes Spektrometer kann die vom Gas ausgehende IR-Strahlung messen. Aus einem solchen Experiment ergibt sich Abbildung 5, ein Diagramm, das bei der Berechnung der Wärmeübertragung von CO₂ in Verbrennungsgasen auf das umschließende Gefäß in einem Ofen, einer Feuerung, einem Kessel, einem Düsentriebwerk usw. hilfreich ist.
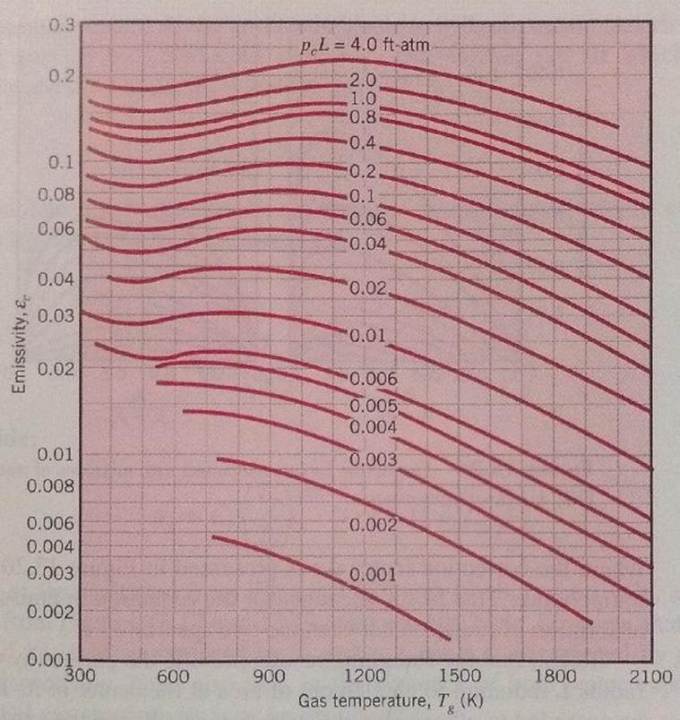
Abbildung 5. Der effektive Emissionsgrad von CO₂ im Gemisch mit nicht teilnehmenden Gasen hängt von Druck, Temperatur und Weglänge ab. Aus Incropera und Dewitt, Fundamentals of heat and Mass Transfer.
Eine Anmerkung zum IR-Spektrum von CO₂
Während wir einen stark absorbierenden CO₂-Übergang bei einer Wellenlänge von etwa 15 μm (den n2-Modus) oft als ein einzelnes Merkmal bezeichnen, ist die Realität dieses Merkmals recht komplex: Der Grund dafür ist, dass die Rotation eines Atoms im Modus n2 die Bindung zwischen O und C streckt, was sich auf die Energie der Biegeschwingung (n2) auswirkt. Es entsteht eine Reihe vieler eng beieinander liegender Linien, die sich im Gesamtdrehimpuls unterscheiden. Es gibt drei Zweige dieser Linie, die als P, Q und R bezeichnet werden. Der Unterschied zwischen den einzelnen Zweigen besteht darin, dass sich der Gesamt-Drehimpuls (J im quantenmechanischen Sprachgebrauch) auf dem P-Zweig während eines Übergangs um -1 ändert. Auf dem Q-Zweig ändert sich J um Null. Auf dem R-Zweig ändert sich J um +1.
Die Linien sind Teil einer sehr feinen Struktur, bei der sich die Wellenzahlen einzelner Linien von denen benachbarter Linien nur um 1 bis 10 cm↑-1 unterscheiden. Ein Spektrometer mit einer Auflösung von mehreren cm-1 oder schlechter kann sie nicht einzeln sehen, sondern nur als eine Art Kontinuum. Ein cm↑-1-Unterschied bei dieser Wellenzahl entspricht einem Frequenzunterschied von etwa 30GHz.
Eine strahlende Oberfläche in Kontakt mit der Atmosphäre
Durch die Zugabe von CO₂ kann unsere Atmosphäre mit einem vorbeiziehenden EM-Feld wechselwirken. Die Betrachtung einer isolierten Spektralkomponente der von der Oberfläche ausgehenden Schwarzkörperstrahlung ist analog zu einer EM-Feldanregung von Gas – wie z. B. in einem Laser. Ein Teil des EM-Feldes wird absorbiert, dann durch Kollisionen deaktiviert, durch andere Kollisionen angeregt und so weiter. Dieses vorbeiziehende EM-Feld erhöht die Population im angeregten Zustand geringfügig über das Maß hinaus, das ein Gleichgewicht bei der Gastemperatur nahelegen würde.
In Segmenten des IR-Spektrums, in denen atmosphärische Komponenten stark absorbieren, wie z. B. im 15-um-CO₂-n2-Komplex, kann ein Spektrometer nur Emissionen aus der unmittelbaren Umgebung erkennen, da die aus der Ferne kommenden absorbiert wurden. Abbildung 6 zeigt dies in dem durch blaue Pfeile gekennzeichneten Segment.
Nicht-Gleichgewichtseffekte von Gradienten
Die von einem CO₂-Atom beim Übergang vom Schwingungszustand in den Grundzustand abgegebene Strahlung ist nicht isotrop, aber es gibt so viele CO₂-Moleküle pro Volumeneinheit der Atmosphäre, die alle zufällig ausgerichtet sind, dass die resultierende Strahlung aus dem Grundmaterial isotrop ist.
In Anbetracht der isotropen Beschaffenheit dieser Strahlung ist es ganz offensichtlich, dass Strahlung, die von Schüttgut aus einem kühleren Ort emittiert wird, auf wärmeres Material, wie z. B. die Bodenoberfläche, treffen und dort absorbiert werden kann. Es gibt kein physikalisches Prinzip, das etwas anderes besagt, und ohne die Berücksichtigung aller dieser Strahlungen ist es nicht möglich, den Nettowärmeübergang korrekt zu bestimmen oder die Energieerhaltung zu erreichen. Die Netto-Wärmeübertragung erfolgt spontan von einer wärmeren Umgebung in eine kältere, selbst wenn man berücksichtigt, dass einzelne Strahlungspakete nicht durch die Temperatur eingeschränkt sind und auch in die andere Richtung gehen können.
Die Energie zur Aufrechterhaltung eines besetzten n2-Zustands ist abhängig von der lokalen Temperatur und der Helligkeit eines vorbeiziehenden EM-Feldes. Die Helligkeit der erzeugten Spektrallinien hängt auch von der Konzentration der strahlenden Spezies ab. Ein Spektrometer, das in eine solche Atmosphäre hineinschaut, wird nicht mehr eine kontinuierliche Schwarzkörperkurve erkennen, sondern eher Segmente oder sogar nicht erkennbare einzelne verbreiterte Linien, deren Helligkeit davon abhängt, welcher Teil der Atmosphäre das beobachtete Spektralmerkmal trägt.
Abbildung 6 zeigt beispielsweise eine von einem Satelliten gemessene spektrografische Messung der Erdoberfläche. In dem durch rote Pfeile markierten breiten Bereich von 800 bis 1200 cm↑-1 sieht die Kurve, abgesehen von einer Einbuchtung im Spektrum bei 1050 cm↑-1, fast wie ein Schwarzkörperspektrum aus einer Quelle bei 290 K aus – also der Erdoberfläche. Dies ist ein klares Fenster in der Atmosphäre, durch welches das Spektrometer die Oberfläche ungehindert sehen kann. Die blauen Pfeile kennzeichnen Abschnitte des Spektrums, in denen CO₂ und H₂O die direkte Sicht auf die Oberfläche blockieren und die spektrale Helligkeit aus den letzten paar Kilometern der CO₂-reichen Atmosphäre nahe der Tropopause (220 K) oder dem oberen Teil der wasserdampfreichen Atmosphäre in etwa 2 km Höhe stammt.
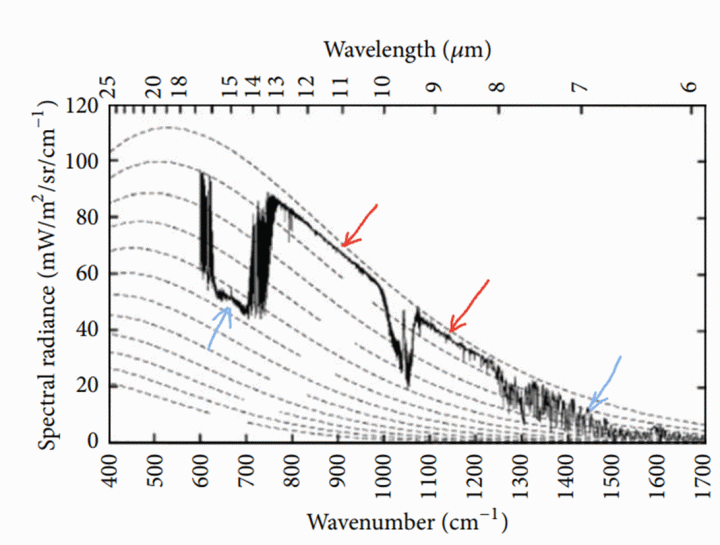
Abbildung 6 aus: Harde, International Journal of Atmospheric Sciences, Volume 2013, Article ID 503727, 26 pages, http://dx.doi.org/10.1155/2013/503727
Die Auswirkungen von Wolken
Wolken bieten ein komplexes Bild. Die winzigen Teilchen, aus denen Wolken bestehen, sind zweifellos manchmal groß genug, um sich wie ein Ensemble kleiner schwarzer Körper zu verhalten, die, wenn sie dicht genug sind, bei der örtlichen Wolkentemperatur selbst wie schwarze Körper wirken würden.
Die Wirkung kleinerer Teilchen in Wolken lenkt die sichtbare Strahlung um. Im Sommer kann man sich im Freien an der Südflanke eines hohen Kumulonimbusturms aufhalten und nicht nur den sehr hellen Himmel im Norden bemerken, sondern auch eine erhöhte Wärme auf der exponierten Haut und auf der Bodenoberfläche, die die Lufttemperatur nicht wesentlich beeinflusst. Siehe zum Beispiel Abbildung 5 in [2].
Viele Wolkenteilchen sind in der Größenordnung der Wellenlängen von Licht und thermischem IR oder etwas größer und streuen Strahlung über Mie-Streuung, aber im Allgemeinen ist die wahre Phasenfunktion für Wolkenstreuung schlecht bekannt. Wijngaarden und Happer (2005) [2] haben einen 2n-Algorithmus formuliert, der die schlecht bekannte Phasenfunktion durch eine Streumatrix ersetzt, die durch Messungen genau bestimmt werden kann. Dicke, tief liegende Wolken lenken thermische IR-Strahlung um, die von der Bodenoberfläche ausgeht.
Zweifellos senken Wolken die Temperatur auf der Erde im Vergleich zu einem wolkenlosen Planeten – eine offensichtliche negative Rückkopplung in diesem Sinne. Aus der Sicht der orthodoxen Klimawissenschaft ist es jedoch dieser große Effekt, der das derzeitige Durchschnittsklima aufrechterhält, und mit Wolkenrückkopplung ist die Auswirkung gemeint, die eine leichte Zunahme der Bewölkung auf den mittleren Klimazustand hätte. Diese Divergenz in den Definitionen gibt Anlass zu vielen Diskussionen.
Wie kühlt sich die Erdoberfläche allein durch IR-Strahlung ab?
Der SB-Rückkopplungsfaktor ist die Zunahme der von einer Oberfläche emittierten Wärmestrahlung aufgrund der steigenden Oberflächentemperatur. Um diesen Faktor zu berechnen, differenziert man einfach das SB-Gesetz in Bezug auf die Temperatur und kehrt das Ergebnis um.
W = σT⁴; wobei σ, die Stefan-Konstante, 5,67×10↑-8 in SI-Einheiten beträgt. Nach der Potenzregel der Differenzierung ist dW/dT dann 4σT³, und sein Kehrwert, dT/dW, beträgt bei 300 K 0,16 K pro W/m^². Mit anderen Worten: Damit das SB-Gesetz bei 300 K ein zusätzliches Watt pro Quadratmeter abstrahlen kann, muss die Oberflächentemperatur nur um 0,16 K erhöht werden.
Das zusätzliche Watt Schwarzkörperstrahlung wird jedoch teilweise von Wasserdampf und Kohlendioxid absorbiert, und ein Teil davon kehrt zum Boden zurück und verhindert die Abkühlung. In diesem Fall des derzeitigen Treibhauseffekts ist ein größerer Temperaturanstieg erforderlich, um ein Watt pro Quadratmeter vollständig in den Weltraum abzustrahlen. In einem vor sechs Jahren veröffentlichten Aufsatz wurde dies damit erklärt, dass die gesamte Atmosphäre wie eine Oberflächenbeschichtung behandelt wird, um der Erde eine bessere „Leistung“ als Sonnenkollektor zu verleihen. Die Atmosphäre verringert den effektiven Emissionsgrad der Oberfläche von nahezu 1,0 auf etwa 0,62. Somit ist die Oberflächenstrahlung tatsächlich W=εσT^⁴; und dT/dW ist 1/(4εσT^³), was bei 300 K 0,26 ist.
Nun kann man argumentieren, dass nicht jeder Ort auf dem Planeten dieselbe „Beschichtung“ hat, aber der Punkt ist, dass es mehr als die von SB abgeleitete Empfindlichkeit von 0,16 K und vielleicht sogar 0,26 K Anstieg der Oberflächentemperatur braucht, um die Oberfläche um ein Watt pro Quadratmeter abzukühlen, es sei denn, es gibt überhaupt keinen lokalen Treibhauseffekt.
Referenzen
- https://www.nesdis.noaa.gov/news/how-atmospheric-sounding-transformed-weather-prediction
- W. A. van Wijngaarden and W. Happer, 2025, Radiation Transport in Clouds, Climate Science, Vol. 5.1 (2025) pp. 1-12.
Link: https://wattsupwiththat.com/2025/06/07/radiation-and-matter/
Übersetzt von Christian Freuer für das EIKE
Der Beitrag Strahlung und Materie erschien zuerst auf EIKE – Europäisches Institut für Klima & Energie.