[Alle Hervorhebungen in diesem Beitrag im Original!]
„Menschen verwenden Begriffe wie ’sicher‘, um ihre Unsicherheit über ein Ereignis zu beschreiben … und Begriffe wie „Zufall“, um ihre Unsicherheit über die Welt zu beschreiben.“ – Mircea Zloteanu
In vielen Bereichen der Wissenschaft wird heute das Wort „Ungewissheit“ in den Mund genommen, ohne dass darüber nachgedacht wird, was mit „Ungewissheit“ gemeint ist, oder zumindest ohne dass dies zum Ausdruck gebracht wird. Diese einfache Tatsache ist so bekannt, dass eine Gruppe in UK mit der Bezeichnung „Sense about Science“ eine Broschüre mit dem Titel „Making Sense of Uncertainty“ (.pdf) veröffentlicht hat. Die Gruppe „Sense about Science“ setzt sich für evidenzbasierte Wissenschaft und Wissenschaftspolitik ein. Die 2013 veröffentlichte Broschüre Making Sense of Uncertainty ist leider ein nur vage getarnter Versuch, den Klimaskeptizismus auf der Grundlage der großen Unsicherheiten in der Klimawissenschaft zu bekämpfen.
Nichtsdestotrotz enthält sie einige grundlegende und notwendige Erkenntnisse über Unsicherheit:
Michael Hanlon: „Wenn die Ungewissheit die Bandbreite der Möglichkeiten sehr groß macht, sollten wir nicht versuchen, eine einzige, präzise Zahl zu ermitteln, da dies einen falschen Eindruck von Gewissheit erweckt – falsche Präzision.“
Ein guter und berechtigter Punkt. Aber das größere Problem ist der „Versuch, eine einzige … Zahl zu finden“, egal ob sie „fälschlich präzise“ ist oder nicht.
David Spiegelhalter: „In der klinischen Medizin können Ärzte nicht genau vorhersagen, was mit jemandem passieren wird, und verwenden daher vielleicht eine Formulierung wie ‚von 100 Menschen wie Ihnen werden 96 die Operation überleben‘. Manchmal gibt es nur so wenige Anhaltspunkte, zum Beispiel weil der Zustand eines Patienten völlig neu ist, dass keine Zahl mit Sicherheit angegeben werden kann.“
Nicht nur in der klinischen Medizin, sondern in vielen Forschungsbereichen werden Arbeiten veröffentlicht, die – trotz vager, sogar widersprüchlicher und begrenzter Beweise mit zugegebenen Schwächen im Studiendesign – endgültige numerische Ergebnisse angeben, die nicht besser als wilde Vermutungen sind. (Siehe die Studien von Jenna Jambeck über Plastik im Meer).
Und, vielleicht die größte Untertreibung und der am wenigsten zutreffende Gesichtspunkt in dieser Broschüre:
„Es besteht eine gewisse Verwirrung zwischen dem wissenschaftlichen und dem alltäglichen Gebrauch der Wörter ‚Unsicherheit‘ und ‚Risiko‘. [Dieser erste Satz stimmt – kh] In der Alltagssprache könnten wir sagen, dass etwas, das unsicher ist, riskant ist. Im wissenschaftlichen Sprachgebrauch bedeutet Risiko jedoch im Großen und Ganzen eine Unsicherheit, die in Bezug auf eine bestimmte Gefahr quantifiziert werden kann – für eine bestimmte Gefahr ist das Risiko also die Wahrscheinlichkeit, dass sie eintritt.“
Viel Konfusion
„Das Risiko ist die Chance, dass es passiert“. Ist das wirklich so? William Briggs weist in seinem Buch „Uncertainty: The Soul of Modeling, Probability & Statistics“ (etwa: Die Seele der Modellierung, Wahrscheinlichkeit und Statistik) darauf hin, dass für eine „Chance“ (d. h. eine „Wahrscheinlichkeit“) zunächst eine Aussage wie „Die Gefahr (der Tod) wird diesem Patienten widerfahren“ und klar dargelegte Prämissen erforderlich sind, von denen die meisten angenommen und nicht dargelegt werden, wie z. B. „Der Patient wird in einem modernen Krankenhaus behandelt, ist ansonsten gesund, der Arzt ist voll qualifiziert und verfügt über umfassende Erfahrung mit dem Verfahren, die Diagnose ist korrekt…“. Ohne vollständige Darlegung der Prämissen kann keine Wahrscheinlichkeitsaussage getroffen werden.
Vor kurzem habe ich hier zwei Aufsätze veröffentlicht, die sich mit der Unsicherheit befassen [Titel übersetzt]:
„Plus oder Minus ist keine Frage“ (hier) und „Grenzen des zentralen Grenzwertsatzes“ (hier).
Jeder von ihnen benutzte fast kindlich einfache Beispiele, um einige sehr grundlegende, wahre Punkte über die Art und Weise darzustellen, wie Ungewissheit verwendet, missbraucht und oft missverstanden wird. Ich hatte mit einem angemessenen Maß an Widerstand gegen diesen unverhohlenen Pragmatismus in der Wissenschaft gerechnet, aber die Heftigkeit und Hartnäckigkeit der Opposition hat mich überrascht. Wenn Sie diese verpasst haben, sehen Sie sich die Aufsätze und ihre Kommentare an. Keiner der Kritiker war in der Lage, ein einfaches Beispiel mit Diagrammen oder Illustrationen zu liefern, um seine konträren (fast immer „statistischen“) Interpretationen und Lösungen zu untermauern.
Wo liegt hier also das Problem?
1. Definition: In der Welt der Statistik wird die Unsicherheit als Wahrscheinlichkeit definiert. „Die Unsicherheit wird durch eine Wahrscheinlichkeitsverteilung quantifiziert, die von unserem Informationsstand über die Wahrscheinlichkeit abhängt, wie hoch der einzelne, wahre Wert der unsicheren Größe ist.“ [Quelle]
[In dem verlinkten Artikel wird die Unsicherheit kontrastiert mit: „Die Variabilität wird durch eine Verteilung der Häufigkeiten mehrerer Instanzen der Größe quantifiziert, die aus beobachteten Daten abgeleitet wird.“]
2. Falsche Anwendung: Die obige Definition wird falsch angewandt, wenn wir die absolute Messunsicherheit betrachten.
Der absolute Fehler oder die absolute Unsicherheit ist die Unsicherheit bei einer Messung, die in den entsprechenden Einheiten ausgedrückt wird.
Die absolute Unsicherheit einer Größe ist der tatsächliche Betrag, um den die Größe unsicher ist, z. B. wenn Länge = 6,0 ± 0,1 cm, ist die absolute Unsicherheit der Länge 0,1 cm. Beachten Sie, dass die absolute Unsicherheit einer Größe die gleichen Einheiten hat wie die Größe selbst.
Anmerkung: Die korrekteste Bezeichnung dafür ist absolute Messunsicherheit. Sie ergibt sich aus dem Messverfahren oder dem Messgerät selbst. Wenn eine Temperatur immer (und nur) in ganzen Grad angegeben wird (oder wenn sie auf ganze Grad gerundet wurde), hat sie eine unausweichliche absolute Messunsicherheit von ± 0,5°. Der als 87° gemeldete/aufgezeichnete Thermometerwert muss also seine Unsicherheit tragen und als „87° ± 0,5°“ angegeben werden – was gleichbedeutend ist mit „irgendeinem Wert zwischen 87,5 und 86,5“ – es gibt eine unendliche Anzahl von Möglichkeiten in diesem Bereich, die alle gleichermaßen möglich sind. (Die natürliche Welt beschränkt die Temperaturen nicht auf die Werte, die genau mit den kleinen Strichen auf den Thermometern übereinstimmen).
Würfeln für die Wissenschaft
Schauen wir uns ein einfaches Beispiel an – einen einzelnen Würfel und ein Würfelpaar zu werfen.
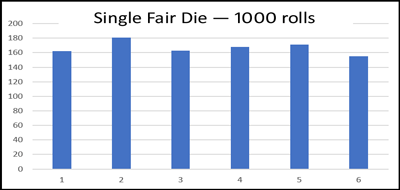
Ein einzelner Würfel (ein Würfel, normalerweise mit leicht abgerundeten Ecken und Kanten) hat sechs Seiten – jede mit einer Anzahl von Punkten: 1, 2, 3, 4, 5 und 6. Wenn er richtig hergestellt ist, hat er eine perfekt gleichmäßige Verteilung der Ergebnisse, wenn viele Male gewürfelt wird. Jede Seite des Würfels (Zahl) wird genauso oft mit der Seite nach oben gefunden wie jede andere Seite (Zahl).
Dies stellt die Verteilung der Ergebnisse von 1.000 Würfen mit einem einzigen fairen Würfel dar. Hätten wir etwa eine Million Mal gewürfelt, lägen die Verteilungswerte der Zahlen näher bei 1:6 für jede Zahl.
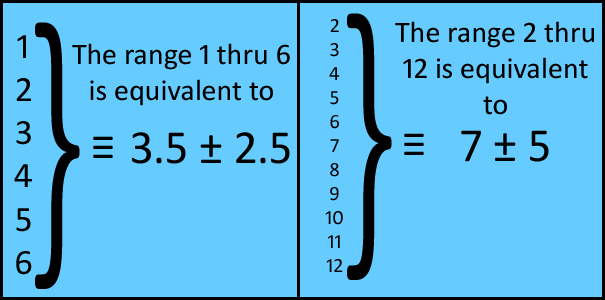
Was ist der Mittelwert der Verteilung? 3.5
Wie groß ist die Spanne des erwarteten Ergebnisses bei einem einzelnen Wurf? 3.5 +/- 2.5
Da jeder Wurf eines Würfels völlig zufällig ist (und innerhalb seiner Parameter nur ganze Werte von 1 bis 6 würfeln kann), können wir für jeden nächsten Wurf den Wert von 3,5 ± 2,5 [nur ganze Zahlen] vorhersagen. Diese Vorhersage wäre zu 100 % korrekt – in diesem Sinne gibt es keinen Zweifel daran, dass der nächste Wurf in diesem Bereich liegen wird, da es nicht anders sein kann.
Da es sich um einen reinen Zufallsprozess handelt, hat jeder Wert, der durch den Bereich „3,5 ± 2,5“ [nur ganze Zahlen] repräsentiert wird, die gleiche Wahrscheinlichkeit, bei jedem „nächsten Wurf“ aufzutreten.
Wie wäre es, wenn wir ein Paar Würfel werfen?
Ein Würfelpaar, zwei der oben beschriebenen Würfel, die gleichzeitig geworfen werden, haben eine Werteverteilung, die wie folgt aussieht:
Wenn wir zwei Würfel werfen, erhalten wir etwas, das wie eine unverzerrte „Normalverteilung“ aussieht. Hätten wir das Würfelpaar eine Million Mal gewürfelt, wäre die Verteilung näher an der vollkommenen Normalverteilung – sehr nahe an der gleichen Anzahl für 3er und 11er und der gleichen Anzahl für 1er wie für 12er.
Welches ist der Mittelwert der Verteilung? 7
Wie groß ist der Bereich des zu erwartenden Ergebnisses bei einem einzelnen Wurf? 7 ± 5
Da jeder Wurf des Würfels völlig zufällig ist (innerhalb seiner Parameter kann er nur ganze Werte von 2 bis 12 würfeln), können wir für jeden nächsten Wurf den Wert „7 ± 5“ vorhersagen.
Aber bei einem Würfelpaar ist die Verteilung nicht mehr gleichmäßig über den gesamten Bereich. Die Werte der Summen der beiden Würfel reichen von 2 bis 12 [nur ganze Zahlen]. 1 ist kein möglicher Wert, ebenso wenig wie eine Zahl über 12. Die Wahrscheinlichkeit, eine 7 zu würfeln, ist viel größer als eine 1 oder 3 oder 11 oder 12 zu würfeln.
Jeder Würfelspieler kann erklären, warum das so ist: Es gibt mehr Kombinationen der Werte der einzelnen Würfel, die 7 ergeben, als solche, die 2 ergeben (es gibt nur eine Kombination für 2: zweimal die 1 und eine Kombination für 12: zweimal die 6).
Würfeln in einer Schachtel
Um aus dem Würfelbeispiel eine echte absolute Messunsicherheit zu machen, bei der wir einen Wert und seine bekannte Unsicherheit angeben, aber den tatsächlichen (oder wahren) Wert nicht kennen (können), legen wir die Würfel in eine geschlossene Schachtel mit einem Deckel. Und dann schütteln wir die Schachtel (würfeln). (Ja, Schrödingers Katze und so weiter.) Wenn wir den Würfel in einen verschlossenen Kasten legen, können wir den Wert nur als eine Menge aller möglichen Werte angeben, oder als Mittelwert ± die oben genannten bekannten Unsicherheiten.
Wir können also unsere Werte für ein Würfelpaar als die Summe der beiden Bereiche für einen einzelnen Würfel betrachten:
Die arithmetische Summe von 3,5 ± 2,5 plus 3,5 ± 2,5 ist eindeutig 7 ± 5. (siehe meine Arbeit „Plus oder Minus ist keine Frage“). Dies ist die korrekte Handhabung der Addition der absoluten Messunsicherheit.
Es wäre genau dasselbe, wenn man zwei Gezeitenmessungen addiert, die eine absolute Messunsicherheit von ± 2 cm haben, oder wenn man zwei Temperaturen addiert, die auf ein ganzes Grad gerundet wurden. Man addiert den Wert und addiert die Unsicherheiten. (Es gibt viele Referenzen dafür. Versuchen Sie es hier.)
Statistiker (als Gruppe) bestehen darauf, dass dies nicht korrekt ist – „Falsch“, wie ein kluger Kommentator bemerkte. Die Statistiker bestehen darauf, dass die korrekte Summe lauten würde:
7 ± 3.5
Einer der Kommentatoren zu Plus oder Minus gab diese statistische Einschätzung ab: „die Unsicherheiten addieren sich IN QUADRATUR. Zum Beispiel: (25,30+/- 0,20) + (25,10 +/- 0,30) = 50,40 +/- SQRT(0,20² + 0,30²) = 50,40 +/-0,36 … Sie würden das Ergebnis als 50,40 +/- 0,36 angeben.
In Worten ausgedrückt: Die Summe der Werte, wobei die Unsicherheit als „Quadratwurzel der Summe der Quadrate der Unsicherheiten“ angegeben wird.
Versuchen wir also, dies auf unser einfaches Würfelproblem mit zwei Würfeln anzuwenden:
(3.5 ± 2.5) + (3.5 ± 2.5) = 7 ± SQRT (2.5² + 2.5²) = 7 ± SQRT(6.25 + 6.25) = 7 ± (SQRT 12.5) = 7 ± 3.5
(Der genauere Wert von √12,5 ist 3,535533905932738…)
Oh je. Das ist etwas ganz anderes als das Ergebnis, wenn man die Regeln für die Addition der absoluten Unsicherheiten befolgt.
Im blauen Diagrammkasten können wir jedoch sehen, dass die korrekte Lösung, die den gesamten Bereich der Unsicherheit einschließt, 7 ± 5 beträgt.
Wo weichen die Ansätze also voneinander ab?
Falsche Annahmen: Der statistische Ansatz verwendet eine Definition, die nicht mit der realen physikalischen Welt übereinstimmt: „Unsicherheit wird durch eine Wahrscheinlichkeitsverteilung quantifiziert“.
So sieht ein Statistiker das Problem:
Wenn es sich jedoch um absolute Messunsicherheiten handelt (oder, wie im Beispiel des Würfelspiels, um absolut bekannte Unsicherheiten – die Unsicherheit ist aufgrund der Beschaffenheit des Systems bekannt), führt die Anwendung der statistischen Regel des „Addierens in Quadratur“ zu einem Ergebnis, das nicht mit der Realität übereinstimmt:
Ein Kommentator des Aufsatzes Grenzen des zentralen Grenzwertsatzes begründete diese Absurdität wie folgt: „Die Wahrscheinlichkeit, dass beide Messungen um den vollen Unschärfewert in dieselbe Richtung abweichen, ist nahezu Null.“
In unserem Würfelbeispiel würden, wenn wir diesen Standpunkt anwenden, die Einsen und Sechsen unserer einzelnen Würfel in einem Paar mit einer Wahrscheinlichkeit von „nahe Null“ zusammenkommen (bei einem Wurf von zwei Würfeln), um die Summen 2 und 12 zu ergeben. 2 und 12 stellen den Mittelwert ± den vollen Unsicherheitswert von plus oder minus 5 dar.
Unser Verteilungsdiagramm der Würfelwürfe zeigt jedoch, dass 2 und 12 nicht einmal selten sind, auch wenn sie seltener vorkommen. Und dennoch können 2er und 12er bei Anwendung der „Quadraturregel“ für die Addition zweier Werte mit absoluter Unsicherheit einfach ignoriert werden. Wir können auch die 3er und 11er ignorieren.
Jeder Würfelspieler weiß, dass dies einfach nicht stimmt, denn die kombinierte Wahrscheinlichkeit, eine 2 oder 3 oder 11 oder 12 zu würfeln, beträgt 18 % – fast 1:5. Eine Wahrscheinlichkeit von 1:5 zu ignorieren, z. B. „die Wahrscheinlichkeit, dass der Fallschirm nicht funktioniert, beträgt 1:5“, ist töricht.
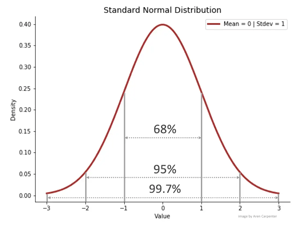
Falls wir die von Statistikern regelmäßig empfohlene „1 Standardabweichung“ (ca. 68 % – gleichmäßig auf beide Seiten des Mittelwerts verteilt) verwenden würden, müssten wir alle 2er, 3er, 11er und 12er und etwa ½ der 3er und 4er aus unserer „Unsicherheit“ eliminieren – die 34 % (>1-in-3) der tatsächlich erwarteten Würfe ausmachen.
Man beachte, dass wir in diesem Beispiel die gewöhnliche Unsicherheit eines zufälligen Ereignisses (Würfelwurf) in eine „absolute Messunsicherheit“ umgewandelt haben, indem wir unsere Würfel in eine Box mit einem Deckel gelegt haben, die uns daran hindert, den tatsächlichen Wert des Würfelwurfs zu kennen, uns aber erlaubt, die gesamte Bandbreite der Unsicherheit zu kennen, die mit der „Messung“ (dem Würfelwurf) verbunden ist. Genau das geschieht, wenn eine Messung „gerundet“ wird – wir verlieren Informationen über den gemessenen Wert und erhalten einen „Wertebereich“. Das Runden auf den „nächsten Dollar“ führt zu einer Unsicherheit von ± 0,50 $; das Runden auf das nächste ganze Grad führt zu einer Unsicherheit von ± 0,5°; das Runden auf die nächsten Jahrtausende führt zu einer Unsicherheit von ± 500 Jahren. Messungen, die mit einem ungenauen Werkzeug oder Verfahren durchgeführt werden, ergeben ebenso dauerhafte Werte mit einer bekannten Unsicherheit.
Diese Art von Unsicherheit lässt sich nicht durch Statistik beseitigen.
Unter dem Strich:
1. Wir scheinen von der Forschung immer eine Zahl zu verlangen – „nur eine Zahl ist am besten“. Dies ist ein miserabler Ansatz für fast jede Forschungsfrage. Der „Trugschluss einer einzigen Zahl“ (den ich, glaube ich, vor kurzem, in diesem Augenblick, geprägt habe. Korrigieren Sie mich, wenn ich falsch liege.) ist „der Glaube, dass komplexe, komplizierte und sogar chaotische Themen und ihre Daten auf eine einzige signifikante und wahrheitsgemäße Zahl reduziert werden können“.
2. Das Beharren darauf, dass alle „Unsicherheit“ ein Maß für die Wahrscheinlichkeit ist, ist eine verzerrte Sicht der Realität. Wir können aus vielen Gründen unsicher sein: „Wir wissen es einfach nicht.“ „Wir haben nur begrenzte Daten“. „Wir haben widersprüchliche Daten.“ „Wir sind uns über die Daten nicht einig.“ „Die Daten selbst sind unsicher, weil sie aus wirklich zufälligen Ereignissen resultieren.“ „Unsere Messinstrumente und -verfahren selbst sind grob und unsicher.“ „Wir wissen nicht genug.“ – Diese Liste ließe sich seitenlang fortsetzen. Fast keiner dieser Umstände lässt sich dadurch korrigieren, dass man so tut, als könne man die Ungewissheit als Wahrscheinlichkeiten darstellen und mit statistischen Ansätzen reduzieren.
3. Die absolute Messunsicherheit ist dauerhaft – sie kann nur durch bessere und/oder genauere Messungen verringert werden.
4. Durchschnittswerte (Mittelwerte und Mediane) neigen dazu, die ursprüngliche Messunsicherheit zu verschleiern und zu verdecken. Durchschnittswerte sind selbst keine Messungen und bilden die Realität nicht richtig ab. Sie sind eine gültige Sichtweise auf einige Daten – verbergen aber oft das umfassendere Bild. (siehe Die Gesetze der Durchschnittswerte)
5. Nur in den seltensten Fällen wird die ursprüngliche Messunsicherheit bei Forschungsergebnissen angemessen berücksichtigt – stattdessen wurde den Forschern beigebracht, sich auf die Vorspiegelung statistischer Ansätze zu verlassen, um ihre Ergebnisse präziser, statistisch signifikanter und damit „wahrer“ erscheinen zu lassen.
——————————–
Kommentar des Autors:
Ich würde mich wirklich freuen, wenn ich in diesem Punkt widerlegt werden würde. Aber bis jetzt hat noch niemand etwas anderes als „mein Statistikbuch sagt …“ vorgelegt. Wer bin ich, dass ich ihren Statistikbüchern widerspreche?
Aber ich behaupte, dass ihre Statistikbücher nicht über das gleiche Thema sprechen (und keine anderen Ansichten zulassen). Man muss schon ziemlich lange suchen, um die korrekte Methode zu finden, mit der zwei Werte mit absoluter Messunsicherheit addiert werden sollen (wie in 10 cm ± 1 cm plus 20 cm ± 5 cm). Es gibt einfach zu viele ähnliche Wörter und Wortkombinationen, die den Internet-Suchmaschinen „gleich erscheinen“. Das Beste, was ich gefunden habe, sind YouTubes zur Physik.
Also, meine Herausforderung an die Herausforderer: Nennen Sie ein kindlich einfaches Beispiel, wie ich es verwendet habe, zwei Messungen mit absoluten Messunsicherheiten, die zueinander addiert werden. Die Arithmetik, ein visuelles Beispiel für die Addition mit Unsicherheiten (auf einer Skala, einem Lineal, einem Thermometer, beim Zählen von Bären, Pokerchips, was auch immer) und zeigen Sie, wie sie physikalisch addiert werden. Wenn Ihre Veranschaulichung gültig ist und du zu einem anderen Ergebnis kommst als ich, dann haben Sie gewonnen! Versuchen Sie es mit den Würfeln. Oder mit einem Zahlenbeispiel, wie es in Plus oder Minus verwendet wird.
Link: https://wattsupwiththat.com/2023/01/03/unknown-uncertain-or-both/
Übersetzt von Christian Freuer für das EIKE